Inequações do 2º grau
(→Inequações do 2º grau) |
(→Inequações do 2º grau) |
||
| (One intermediate revision by one user not shown) | |||
| Line 1: | Line 1: | ||
==Inequações do 2º grau== | ==Inequações do 2º grau== | ||
| − | |||
O gráfico da função $f(x)=ax^2+bx+c$, com $a\neq0$, é uma parábola. Se $a<0$ a concavidade da parábola é voltada para baixo e se $a>0$ a concavidade é voltada para cima. | O gráfico da função $f(x)=ax^2+bx+c$, com $a\neq0$, é uma parábola. Se $a<0$ a concavidade da parábola é voltada para baixo e se $a>0$ a concavidade é voltada para cima. | ||
| Line 12: | Line 11: | ||
[[File:parabolas1.jpg]] Neste caso temos a concavidade voltada para cima, por isso $a>0$ e a parábola interseta o eixo das abcissas em dois pontos, portanto $\Delta > 0$. O vértice da parábola tem uma ordenada negativa. [[Exemplo-8|(Exemplo)]] | [[File:parabolas1.jpg]] Neste caso temos a concavidade voltada para cima, por isso $a>0$ e a parábola interseta o eixo das abcissas em dois pontos, portanto $\Delta > 0$. O vértice da parábola tem uma ordenada negativa. [[Exemplo-8|(Exemplo)]] | ||
| − | |||
[[File:parabolas2.jpg]] Neste caso temos a concavidade voltada para cima, por isso $a>0$ e a parábola interseta o eixo das abcissas apenas num ponto, portanto $\Delta = 0$. O vértice da parábola é o seu zero. [[Exemplo-9|(Exemplo)]] | [[File:parabolas2.jpg]] Neste caso temos a concavidade voltada para cima, por isso $a>0$ e a parábola interseta o eixo das abcissas apenas num ponto, portanto $\Delta = 0$. O vértice da parábola é o seu zero. [[Exemplo-9|(Exemplo)]] | ||
| − | |||
| − | |||
[[File:parabolas3.jpg]] Neste caso temos a concavidade voltada para cima, por isso $a>0$ e a parábola não interseta o eixo das abcissas, portanto $\Delta < 0$. [[Exemplo-10|(Exemplo)]] | [[File:parabolas3.jpg]] Neste caso temos a concavidade voltada para cima, por isso $a>0$ e a parábola não interseta o eixo das abcissas, portanto $\Delta < 0$. [[Exemplo-10|(Exemplo)]] | ||
| − | |||
| − | |||
[[File:parabolas4.jpg]] Neste caso temos a concavidade voltada para baixo, por isso $a<0$ e a parábola interseta o eixo das abcissas em dois pontos, logo $\Delta >0$. [[Exemplo-13|(Exemplo)]] | [[File:parabolas4.jpg]] Neste caso temos a concavidade voltada para baixo, por isso $a<0$ e a parábola interseta o eixo das abcissas em dois pontos, logo $\Delta >0$. [[Exemplo-13|(Exemplo)]] | ||
| − | |||
| − | |||
[[File:parabolas5.jpg]] Neste caso temos a concavidade voltada para baixo, por isso $a<0$ e a parábola interseta o eixo das abcissas apenas num ponto, logo $\Delta =0$. [[Exemplo-11|(Exemplo)]] | [[File:parabolas5.jpg]] Neste caso temos a concavidade voltada para baixo, por isso $a<0$ e a parábola interseta o eixo das abcissas apenas num ponto, logo $\Delta =0$. [[Exemplo-11|(Exemplo)]] | ||
| − | |||
| − | |||
[[File:parabolas6.jpg]] Neste caso temos a concavidade voltada para baixo, por isso $a<0$ e a parábola não interseta o eixo das abcissas, logo $\Delta <0$. [[Exemplo-12|(Exemplo)]] | [[File:parabolas6.jpg]] Neste caso temos a concavidade voltada para baixo, por isso $a<0$ e a parábola não interseta o eixo das abcissas, logo $\Delta <0$. [[Exemplo-12|(Exemplo)]] | ||
| + | [[Exercícios-9|Exercícios]] | ||
| − | + | [[Matemática Elementar#Inequações|Voltar]] [[Inequações com módulos|Seguinte]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | # | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
Latest revision as of 16:23, 16 November 2012
[edit] Inequações do 2º grau
O gráfico da função $f(x)=ax^2+bx+c$, com $a\neq0$, é uma parábola. Se $a<0$ a concavidade da parábola é voltada para baixo e se $a>0$ a concavidade é voltada para cima.
Resolver a inequação $ax^2+bx+c > 0$ é determinar os valores de $x$ para os quais a função $f$ é positiva, isto é, o gráfico da função fica acima do eixo dos $xx$.
Analogamente, resolver a inequação $ax^2+bx+c<0$ é determinar os valores de $x$ para os quais a função é negativa, ou seja, o gráfico da função fica abaixo do eixo dos $xx$.
As soluções deste tipo de inequações dependem do valor de $a$ e da posição do vértice da parábola correspondente à inequação tal como ilustram as tabelas seguintes. Recorde-se que a ordenada do vértice é dada por $y_v=\displaystyle -\frac{\Delta}{4a}$ e a abcissa é $\displaystyle x_v=-\frac{b}{2a}$, com $\Delta = b^2-4ac$.
Por exemplo a parábola $y=3x^2$, tem o vértice em $(0,0)$ e a concavidade voltada para cima, enquanto que a parábola $y=-3x^2$ tem o mesmo vértice mas a concavidade voltada para baixo.
Neste caso temos a concavidade voltada para cima, por isso $a>0$ e a parábola interseta o eixo das abcissas em dois pontos, portanto $\Delta > 0$. O vértice da parábola tem uma ordenada negativa. (Exemplo)
Neste caso temos a concavidade voltada para cima, por isso $a>0$ e a parábola interseta o eixo das abcissas apenas num ponto, portanto $\Delta = 0$. O vértice da parábola é o seu zero. (Exemplo)
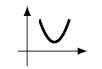Neste caso temos a concavidade voltada para cima, por isso $a>0$ e a parábola não interseta o eixo das abcissas, portanto $\Delta < 0$. (Exemplo)
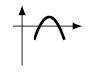Neste caso temos a concavidade voltada para baixo, por isso $a<0$ e a parábola interseta o eixo das abcissas em dois pontos, logo $\Delta >0$. (Exemplo)
Neste caso temos a concavidade voltada para baixo, por isso $a<0$ e a parábola interseta o eixo das abcissas apenas num ponto, logo $\Delta =0$. (Exemplo)
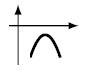Neste caso temos a concavidade voltada para baixo, por isso $a<0$ e a parábola não interseta o eixo das abcissas, logo $\Delta <0$. (Exemplo)
