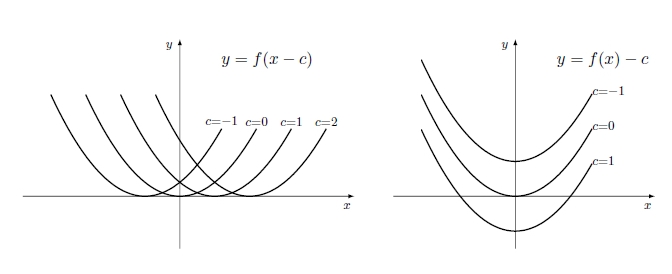Translações de gráficos
From Matemática
(Difference between revisions)
(Created page with "==Translações de gráficos de funções== Dada uma função $f:D_f\subseteq \mathbb{R}\rightarrow \mathbb{R}$ podemos obter uma nova função fazendo uma translação do gr...") |
(→Translações de gráficos de funções) |
||
| Line 19: | Line 19: | ||
de $f$ sobre o eixo dos $yy$ segundo $(0,c)$ (para cima se $c<0$ e para baixo se $c > 0$). | de $f$ sobre o eixo dos $yy$ segundo $(0,c)$ (para cima se $c<0$ e para baixo se $c > 0$). | ||
| − | [[Matemática Elementar#Funções reais de variável real|Voltar]] | + | [[Matemática Elementar#Funções reais de variável real|Voltar]] [[Função composta|Seguinte]] |
Revision as of 09:21, 19 November 2012
Translações de gráficos de funções
Dada uma função $f:D_f\subseteq \mathbb{R}\rightarrow \mathbb{R}$ podemos obter uma nova função fazendo uma translação do gráfico de $f$ ao longo do eixo das abcissas ou ao longo do eixo das ordenadas, $g(x)=f(x-c)$ ou $g(x)=f(x)-c$, em que $c$ é um parâmetro real.
No caso $g(x)=f(x-c)$, o domínio de $g$ é
$$D_g=\{x \in \mathbb{R}: x-c \in D_f \}.$$
Se $g(x)=f(x)-c$, o domínio de $g$ coincide com o domínio de $f$.
$g(x)=f(x-c)$ representa uma translação
de $f$ sobre o eixo dos $xx$ segundo $(c,0)$ (para a direita se $c>0$ e para a
esquerda se $c < 0$).
$g(x)=f(x)-c$ representa uma translação de $f$ sobre o eixo dos $yy$ segundo $(0,c)$ (para cima se $c<0$ e para baixo se $c > 0$).