Funções reais de variável real
(Created page with "Se $A\subseteq \mathbb{R}$ e $B=\mathbb{R}$, a função $f:A\rightarrow B$ diz-se \textbf{função real de variável real}. Usar-se-ão as notações $D_f$ para domínio da fu...") |
|||
| (22 intermediate revisions by one user not shown) | |||
| Line 1: | Line 1: | ||
| − | Se $A\subseteq \mathbb{R}$ e $B=\mathbb{R}$, a função $f:A\rightarrow B$ diz-se | + | Se $A\subseteq \mathbb{R}$ e $B=\mathbb{R}$, a função $f:A\rightarrow B$ diz-se '''função real |
| − | de variável real | + | de variável real'''. |
Usar-se-ão as notações $D_f$ para domínio da função $f$ e $CD_f$ para contradomínio de $f$ e indica-se $f:D_f\subseteq \mathbb{R}\longrightarrow \mathbb{R}$. | Usar-se-ão as notações $D_f$ para domínio da função $f$ e $CD_f$ para contradomínio de $f$ e indica-se $f:D_f\subseteq \mathbb{R}\longrightarrow \mathbb{R}$. | ||
| − | + | O contradomínio de $f$ é o conjunto | |
| − | + | <blockquote> | |
$CD_f=f(D_f)=\{ f(x) : x \in D_f \}=\{ y \in \mathbb{R}:y=f(x) \wedge x \in D_f \}$ | $CD_f=f(D_f)=\{ f(x) : x \in D_f \}=\{ y \in \mathbb{R}:y=f(x) \wedge x \in D_f \}$ | ||
| − | + | </blockquote> | |
Frequentemente uma função é dada por uma regra $y=f(x)$, significando que a cada valor da variável independente $x$ se associa um valor da variável dependente $y=f(x)$. Por exemplo, se a regra é $f(x)=x^2$, a cada valor de $x$ é associado o seu quadrado, por exemplo | Frequentemente uma função é dada por uma regra $y=f(x)$, significando que a cada valor da variável independente $x$ se associa um valor da variável dependente $y=f(x)$. Por exemplo, se a regra é $f(x)=x^2$, a cada valor de $x$ é associado o seu quadrado, por exemplo | ||
| − | + | <blockquote> | |
| − | + | {| class="wikitable" style="text-align:center" | |
| − | y | + | |- |
| − | + | |width="20pt" | $x$ ||width="20pt"| $0$ || width="20pt"| $-2$ ||width="20pt"| $-1$ ||width="20pt"| $1$ ||width="20pt"| $2$ ||width="20pt"| $3$ ||width="20pt"| $\displaystyle \frac{4}{5}$ | |
| − | + | |- | |
| − | + | | $y$ || $0$ || $4$ || $1$ || $1$ || $4$ || $9$ || $\displaystyle \frac{16}{25}$ | |
| − | + | |} | |
| + | </blockquote> | ||
| − | \ | + | Quando a função é dada pela sua expressão analítica, |
| + | o domínio é o '''maior''' subconjunto de $\mathbb{R}$ onde a expressão tem significado. | ||
| + | Por exemplo, a função $g(x)= x^3-3x$ tem domínio $D_g=\mathbb{R}$ e a função $\displaystyle h(x)=\frac{1}{x-1}$ tem domínio $D_h=\mathbb{R}\setminus\{1\}$. | ||
| − | + | Chama-se '''gráfico de uma função $f$''', real de | |
variável real, ao subconjunto de $\mathbb{R}^2$ definido por | variável real, ao subconjunto de $\mathbb{R}^2$ definido por | ||
| − | + | ||
| + | <blockquote> | ||
$Gr_f=\{ (x, \; y) \in \mathbb{R}^2: \ x \in D_f \mbox{ e } y=f(x)\}.$ | $Gr_f=\{ (x, \; y) \in \mathbb{R}^2: \ x \in D_f \mbox{ e } y=f(x)\}.$ | ||
| − | + | </blockquote> | |
| + | |||
Para obter o gráfico de uma função marcam-se num referencial no plano $\mathbb{R}^2$ pares ordenados de pontos $(x,f(x))$. No eixo horizontal (eixo das abcissas) marcam-se os valores $x$ do domínio de $f$ e no eixo vertical (eixo das ordenadas) marcam-se os valores correspondentes para $f(x)$ (o contradomínio de $f$). | Para obter o gráfico de uma função marcam-se num referencial no plano $\mathbb{R}^2$ pares ordenados de pontos $(x,f(x))$. No eixo horizontal (eixo das abcissas) marcam-se os valores $x$ do domínio de $f$ e no eixo vertical (eixo das ordenadas) marcam-se os valores correspondentes para $f(x)$ (o contradomínio de $f$). | ||
| + | |||
| + | [[File:funcao1.jpg]] | ||
| + | |||
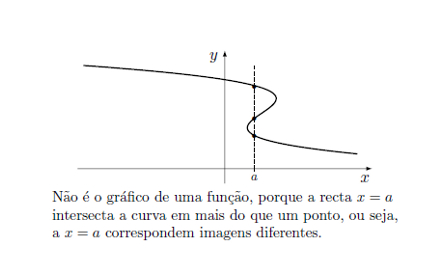
| + | Para que uma curva represente o gráfico de uma função, qualquer reta vertical interseta a curva no máximo num ponto (pode não intersetar em nenhum, caso o domínio da função não seja $\mathbb{R}$). | ||
| + | |||
| + | [[File:naofunc1.jpg]] [[File:naofunc2.jpg]] | ||
| + | |||
| + | [[Matemática Elementar#Funções reais de variável real|Voltar]] [[Zeros e sinal de uma função|Seguinte]] | ||
Latest revision as of 16:26, 6 February 2013
Se $A\subseteq \mathbb{R}$ e $B=\mathbb{R}$, a função $f:A\rightarrow B$ diz-se função real de variável real. Usar-se-ão as notações $D_f$ para domínio da função $f$ e $CD_f$ para contradomínio de $f$ e indica-se $f:D_f\subseteq \mathbb{R}\longrightarrow \mathbb{R}$.
O contradomínio de $f$ é o conjunto
$CD_f=f(D_f)=\{ f(x) : x \in D_f \}=\{ y \in \mathbb{R}:y=f(x) \wedge x \in D_f \}$
Frequentemente uma função é dada por uma regra $y=f(x)$, significando que a cada valor da variável independente $x$ se associa um valor da variável dependente $y=f(x)$. Por exemplo, se a regra é $f(x)=x^2$, a cada valor de $x$ é associado o seu quadrado, por exemplo
$x$ $0$ $-2$ $-1$ $1$ $2$ $3$ $\displaystyle \frac{4}{5}$ $y$ $0$ $4$ $1$ $1$ $4$ $9$ $\displaystyle \frac{16}{25}$
Quando a função é dada pela sua expressão analítica, o domínio é o maior subconjunto de $\mathbb{R}$ onde a expressão tem significado. Por exemplo, a função $g(x)= x^3-3x$ tem domínio $D_g=\mathbb{R}$ e a função $\displaystyle h(x)=\frac{1}{x-1}$ tem domínio $D_h=\mathbb{R}\setminus\{1\}$.
Chama-se gráfico de uma função $f$, real de variável real, ao subconjunto de $\mathbb{R}^2$ definido por
$Gr_f=\{ (x, \; y) \in \mathbb{R}^2: \ x \in D_f \mbox{ e } y=f(x)\}.$
Para obter o gráfico de uma função marcam-se num referencial no plano $\mathbb{R}^2$ pares ordenados de pontos $(x,f(x))$. No eixo horizontal (eixo das abcissas) marcam-se os valores $x$ do domínio de $f$ e no eixo vertical (eixo das ordenadas) marcam-se os valores correspondentes para $f(x)$ (o contradomínio de $f$).
Para que uma curva represente o gráfico de uma função, qualquer reta vertical interseta a curva no máximo num ponto (pode não intersetar em nenhum, caso o domínio da função não seja $\mathbb{R}$).