Função módulo
From Matemática
(Difference between revisions)
(→A função módulo) |
(→A função módulo) |
||
| (One intermediate revision by one user not shown) | |||
| Line 6: | Line 6: | ||
| − | Esta função é contínua (o gráfico não tem "saltos"), tem um zero em $x=0$, é decrescente em $]-\infty,0[$ e crescente em $]0,+\infty[$. $(0,f(0))=(0,0)$ é um mínimo local e | + | Esta função é contínua (o gráfico não tem "saltos"), tem um zero em $x=0$, é decrescente em $]-\infty,0[$ e crescente em $]0,+\infty[$. $(0,f(0))=(0,0)$ é um mínimo local e absoluto da função. |
| Line 15: | Line 15: | ||
[[Exercícios 4|Exercícios propostos]] | [[Exercícios 4|Exercícios propostos]] | ||
| − | [[Matemática Elementar#Funções reais de variável real|Voltar]] [[Seguinte]] | + | [[Matemática Elementar#Funções reais de variável real|Voltar]] [[Translações de gráficos|Seguinte]] |
Latest revision as of 19:53, 12 February 2013
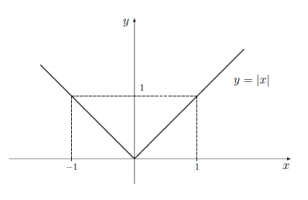
[edit] A função módulo
A função módulo pode ser encarada como uma função definida por ramos:
Esta função é contínua (o gráfico não tem "saltos"), tem um zero em $x=0$, é decrescente em $]-\infty,0[$ e crescente em $]0,+\infty[$. $(0,f(0))=(0,0)$ é um mínimo local e absoluto da função.
A representação gráfica da função módulo pode ajudar na resolução de problemas algébricos, como o exemplo seguinte ilustra.