|
|
| (4 intermediate revisions by one user not shown) |
| Line 6: |
Line 6: |
| | | | |
| | | | |
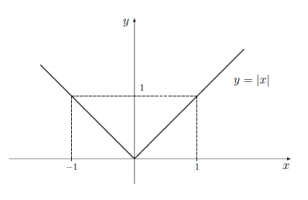
| − | Esta função é contínua (o gráfico não tem "saltos"), tem um zero em $x=0$, é decrescente em $]-\infty,0[$ e crescente em $]0,+\infty[$. $(0,f(0))=(0,0)$ é um mínimo local e global da função. | + | Esta função é contínua (o gráfico não tem "saltos"), tem um zero em $x=0$, é decrescente em $]-\infty,0[$ e crescente em $]0,+\infty[$. $(0,f(0))=(0,0)$ é um mínimo local e absoluto da função. |
| | | | |
| | | | |
| | A representação gráfica da função módulo pode ajudar na resolução de problemas algébricos, como o exemplo seguinte ilustra. | | A representação gráfica da função módulo pode ajudar na resolução de problemas algébricos, como o exemplo seguinte ilustra. |
| | | | |
| − | [[Exemplo 18|Exemplo]] | + | [[Exemplo 18|Exemplo]] [[Outros exemplos]] |
| | | | |
| | + | [[Exercícios 4|Exercícios propostos]] |
| | | | |
| − | [[Outros exemplos]] | + | [[Matemática Elementar#Funções reais de variável real|Voltar]] [[Translações de gráficos|Seguinte]] |
| − | | + | |
| − | | + | |
| − | \subsubsection*{Exercícios Resolvidos}
| + | |
| − | Seja $f$ a função definida por $f(x)=|x^2-3x+2|$.
| + | |
| − | \begin{description}
| + | |
| − | \item[(a)] Reescreva a expressão analítica de $f$ sem usar o símbolo $|\ |$.
| + | |
| − | \item[(b)]Determine o conjunto $A\subseteq \mathbb{R}$ por forma a que a proposição ``$f(x)<1, \mbox{ se e só se } x \in A$" \ seja verdadeira.
| + | |
| − | \end{description}
| + | |
| − | \textbf{Resolução:} \begin{description}
| + | |
| − | \item[(a)] Comecemos por analisar o sinal de $x^2-3x+2$.
| + | |
| − | $$x^2-3x+2=0 \Leftrightarrow x=\frac{3\pm \sqrt{9-8}}{2}\Leftrightarrow x=2 \vee x=1.
| + | |
| − | \mbox{ Assim, }x^2-3x+2=(x-2)(x-1).$$
| + | |
| − | O produto será positivo se os dois factores tiverem o mesmo sinal e negativo se os factores tiverem sinais contrários. Então:
| + | |
| − | $$\begin{array}{c|c|c|c|c|c}
| + | |
| − | &\hspace{1cm} & 1 & \hspace{1cm} & 2 & \hspace{1cm} \\ \hline | + | |
| − | x-1 & - & 0 & + & + & + \\ \hline
| + | |
| − | x-2 & - & - & - & 0 & + \\ \hline
| + | |
| − | (x-1)(x-2)& + & 0 & - & 0 & + \\
| + | |
| − | \end{array}$$
| + | |
| − | | + | |
| − | $$\begin{array}{c}
| + | |
| − | x^2-3x+2=(x-2)(x-1) > 0 \mbox{ se } x \in ]- \infty , 1 [ \cup ]2, + \infty[ \\
| + | |
| − | \mbox{ e } \\
| + | |
| − | x^2-3x+2=(x-2)(x-1) < 0 \mbox{ se } x \in ]1,2[
| + | |
| − | \end{array}$$
| + | |
| − | Podemos agora definir a função $f$ por ramos da seguinte forma:
| + | |
| − | $$f(x)= \left \{ \begin{array}{lll}
| + | |
| − | x^2-3x+2 & \mbox{ se } & x \leq 1 \vee x > 2 \\
| + | |
| − | & & \\
| + | |
| − | -x^2+3x-2 & \mbox{ se } & 1 < x \leq 2 \\
| + | |
| − | \end{array}
| + | |
| − | \right.$$
| + | |
| − | Repare que $f(1)=f(2)=0$ sendo portanto indiferente calcular o valor da função nestes pontos num ou noutro ramo.
| + | |
| − | \item[(b)] Pretende-se determinar o conjunto
| + | |
| − | $$A =\{x \in \mathbb{R}: |x^2-3x+2|<1 \}=\{x \in \mathbb{R}: -1<x^2-3x+2<1 \}$$
| + | |
| − | Resolvendo as duas inequações temos:
| + | |
| − | {\small
| + | |
| − | $$\begin{array}{l||l}
| + | |
| − | -1<x^2-3x+2\Leftrightarrow x^2-3x+3 > 0 & x^2-3x+2<1\Leftrightarrow x^2-3x+1<0 \\
| + | |
| − | & \\
| + | |
| − | \mbox{A equação }x^2-3x+3 = 0 \mbox{ não tem raízes } & \mbox{A equação }x^2-3x+1 = 0 \mbox{ admite as raízes } \\
| + | |
| − | \mbox{reais.}&\DS x= \frac{3-\sqrt{5}}{2} \mbox{ e } x= \frac{3+\sqrt{5}}{2}.\\
| + | |
| − | \mbox{Portanto }x^2-3x+3 > 0, \forall x \in \mathbb{R} & \mbox{Portanto }x^2-3x+1 < 0, \forall x \in \DS \left ] \frac{3-\sqrt{5}}{2} , \frac{3+\sqrt{5}}{2}\right[\\
| + | |
| − | \end{array}$$
| + | |
| − | }
| + | |
| − | O conjunto $A $ é a intersecção dos conjuntos solução das duas inequações,
| + | |
| − | $$A=\mathbb{R}\cap \DS \left ] \frac{3-\sqrt{5}}{2} , \frac{3+\sqrt{5}}{2}\right[ = \DS \left ] \frac{3-\sqrt{5}}{2} , \frac{3+\sqrt{5}}{2}\right[$$
| + | |
| − | \end{description}
| + | |
| − | | + | |
| − | | + | |
| − | \subsubsection*{Exercícios Propostos}
| + | |
| − | \begin{enumerate}
| + | |
| − | \item Reescreva a expressão analítica das seguintes funções, sem usar o símbolo módulo:
| + | |
| − | \begin{description}
| + | |
| − | \item[(a)] $f(x)=|x-1|$;
| + | |
| − | \item[(b)] $g(x)=|x|-3.$
| + | |
| − | \end{description}
| + | |
| − | \item
| + | |
| − | Utilize o processo gráfico para resolver as inequações:
| + | |
| − | \begin{description}
| + | |
| − | \item[(a)] $|x^2-1|\le x+1$;
| + | |
| − | \item[(b)] $|2-x| \ge 2-|x+3|$.
| + | |
| − | \end{description}
| + | |
| − | \end{enumerate}
| + | |
Esta função é contínua (o gráfico não tem "saltos"), tem um zero em $x=0$, é decrescente em $]-\infty,0[$ e crescente em $]0,+\infty[$. $(0,f(0))=(0,0)$ é um mínimo local e absoluto da função.