|
|
| (2 intermediate revisions by one user not shown) |
| Line 15: |
Line 15: |
| | Formalmente, dizemos que '''a sucessão converge para $L$''' se | | Formalmente, dizemos que '''a sucessão converge para $L$''' se |
| | $$\forall \epsilon >0, \hspace{.2cm }\exists N \in \mathbb{N} \hspace{.2cm}: | | $$\forall \epsilon >0, \hspace{.2cm }\exists N \in \mathbb{N} \hspace{.2cm}: |
| − | \hspace{.2cm} n \geq N \to |a_n-L|< \epsilon$$ | + | \hspace{.2cm} n \geq N \Rightarrow |a_n-L|< \epsilon$$ |
| | Se tal real $L$ não existe, dizemos que a sucessão é '''divergente'''. | | Se tal real $L$ não existe, dizemos que a sucessão é '''divergente'''. |
| | | | |
| Line 38: |
Line 38: |
| | | | |
| | Se $\lim a_n=+ \infty$ dizemos que a sucessão $(a_n)_n$ é um '''infinitamente grande positivo'''. Formalmente dizemos, | | Se $\lim a_n=+ \infty$ dizemos que a sucessão $(a_n)_n$ é um '''infinitamente grande positivo'''. Formalmente dizemos, |
| − | $$\lim a_n=+ \infty \Leftrightarrow \forall M \in \mathbb{R}, \hspace{.2cm} \exists N \in \mathbb{N} \hspace{.2cm}: \hspace{.2cm} n \geq N \to a_n>M;$$ | + | $$\lim a_n=+ \infty \Leftrightarrow \forall M \in \mathbb{R}, \hspace{.2cm} \exists N \in \mathbb{N} \hspace{.2cm}: \hspace{.2cm} n \geq N \Rightarrow a_n>M;$$ |
| | Se $\lim a_n=- \infty$ a sucessão diz-se um '''infinitamente grande negativo'''. Formalmente temos: | | Se $\lim a_n=- \infty$ a sucessão diz-se um '''infinitamente grande negativo'''. Formalmente temos: |
| | $$\lim a_n=- \infty \Leftrightarrow\forall M \in \mathbb{R}, \hspace{.2cm} \exists N \in \mathbb{N} \hspace{.2cm}: \hspace{.2cm} | | $$\lim a_n=- \infty \Leftrightarrow\forall M \in \mathbb{R}, \hspace{.2cm} \exists N \in \mathbb{N} \hspace{.2cm}: \hspace{.2cm} |
| − | n \geq N \to a_n<M;$$ | + | n \geq N \Rightarrow a_n<M;$$ |
| | Se $\lim a_n=0$ a sucessão é um '''infinitésimo'''. Formalmente, | | Se $\lim a_n=0$ a sucessão é um '''infinitésimo'''. Formalmente, |
| | $$\lim a_n=0 \Leftrightarrow | | $$\lim a_n=0 \Leftrightarrow |
| | \forall \epsilon >0, \hspace{.2cm} \exists N \in \mathbb{N} \hspace{.2cm}: \hspace{.2cm} | | \forall \epsilon >0, \hspace{.2cm} \exists N \in \mathbb{N} \hspace{.2cm}: \hspace{.2cm} |
| − | n \geq N \to |a_n|< \epsilon.$$ | + | n \geq N \Rightarrow |a_n|< \epsilon.$$ |
| | | | |
| | | | |
| | | | |
| − | \subsection{Limites notáveis}
| + | [[Matemática Elementar#Sucessões|Voltar]] [[Limites notáveis|Seguinte]] |
| − | Segue a lista de alguns limites ``notáveis", i.e., alguns dos limites frequentemente usados e cuja determinação não é simples.
| + | |
| − | \begin{itemize}
| + | |
| − | \item{$\displaystyle \lim \frac{1}{n}=0$,}
| + | |
| − | \item{$\displaystyle \lim \sqrt[n]{a}=1$, onde $a>0$;}
| + | |
| − | \item{$\displaystyle \lim \sqrt[n]{n}=1$;}
| + | |
| − | \item{$\displaystyle \lim a^n \left\{\begin{array}{lll}
| + | |
| − | = 0 & \mbox{ se } & -1<a<1\\
| + | |
| − | = 1 & \mbox{ se } & a=1\\
| + | |
| − | = +\infty & \mbox{ se } & a>1 \\
| + | |
| − | \mbox{ não existe } & \mbox{ se } & a \leq -1 \\
| + | |
| − | \end{array}
| + | |
| − | \right. $
| + | |
| − | }
| + | |
| − | \item{$\displaystyle \lim \left(
| + | |
| − | 1+ \frac{a}{n}\right)^n=e^a.$}
| + | |
| − | | + | |
| − | \end{itemize}
| + | |
| − | | + | |
| − | \subsection{Propriedades aritméticas dos limites}
| + | |
| − | Sejam $(a_n)_n$ e $(b_n)_n$ duas sucessões convergentes, tais que $\lim a_n=a$ e $\lim b_n=b$, com $a,b \in \mathbb{R}$. Então
| + | |
| − | \begin{enumerate}
| + | |
| − | \item{$\displaystyle \lim(a_n \pm b_n)=a \pm b$;}
| + | |
| − | \item{$\displaystyle \lim(a_n\cdot b_n)=a \cdot b$;}
| + | |
| − | \item{$\displaystyle \lim\frac{a_n}{b_n}=\frac{a}{b}$ se $b \not=0$;}
| + | |
| − | \end{enumerate}
| + | |
| − | | + | |
| − | \textbf{Observação:} Se $a= \pm \infty$ e $b \in \mathbb{R}$, então:
| + | |
| − | \begin{itemize}
| + | |
| − | \item $\displaystyle \lim(a_n \pm b_n)=\pm \infty$;
| + | |
| − | \item Se $b \neq 0$ então $\displaystyle \lim(a_n\cdot b_n)=\pm \infty$, dependendo do sinal de $b$.
| + | |
| − | \item Se $b \neq 0$ então $\displaystyle \lim\frac{a_n}{b_n}=\pm \infty$, dependendo do sinal de $b$.
| + | |
| − | \end{itemize}
| + | |
| − | | + | |
| − | \subsection{Teoremas sobre limites}
| + | |
| − | | + | |
| − | | + | |
| − | \textbf{Teorema:} Toda a sucessão limitada e monótona é convergente.
| + | |
| − | | + | |
| − | \vspace{3mm}
| + | |
| − | Este resultado não nos permite determinar o limite mas garante a sua existência. Frequentemente é usado em sucessões definidas por recorrência.
| + | |
| − | | + | |
| − | \vspace{5mm}
| + | |
| − | \textbf{Teorema:} Sejam $(a_n)_n$ e $(b_n)_n$ duas sucessões convergentes para $a$ e $b$ respectivamente. Se a partir de certa ordem, se verifica $a_n\le b_n$, então $a
| + | |
| − | \leq b$.
| + | |
| − | | + | |
| − | \vspace{5mm}
| + | |
| − | \textbf{Teorema das sucessões enquadradas} Dadas três sucessões $(a_n)_{n \in \mathbb{N}}$, $(b_n)_{n \in \mathbb{N}}$ e
| + | |
| − | $(c_n)_{n \in \mathbb{N}}$ tais que
| + | |
| − | \begin{enumerate}
| + | |
| − | \item{$a_n \leq b_n \leq c_n$, a partir de certa ordem;}
| + | |
| − | \item{$\lim a_n = \lim c_n$,}
| + | |
| − | \end{enumerate}
| + | |
| − | então existe $\lim b_n$ e $\lim a_n= \lim b_n = \lim c_n$.
| + | |
| − | | + | |
| − | | + | |
| − | | + | |
| − | \subsubsection*{Exercícios Resolvidos}
| + | |
| − | | + | |
| − | Calcule o limite das seguintes sucessões:
| + | |
| − | \begin{description}
| + | |
| − | \item[(a)]{$\displaystyle a_n=\frac{3n-5}{n+1}$.}
| + | |
| − | \item[(b)]{$\displaystyle b_n=\frac{4n^5+3n^2-n-5}{3n^2-2n+10}$.}
| + | |
| − | \item[(c)]{$\displaystyle c_n=-n^2+n+7$.}
| + | |
| − | \item[(d)]{$\displaystyle d_n=\frac{2^n-3^{n+2}}{2^{n-1}+3^{n+1}}$.}
| + | |
| − | \item[(e)]{$\displaystyle e_n= \sin (n \pi)$.}
| + | |
| − | \item[(f)]{$\displaystyle f_n= \sin \left( \frac{n \pi}{2} \right)$.}
| + | |
| − | \item[(g)]{$\displaystyle g_n=\frac{(-1)^{n+3}n+1}{n^3+1}$.}
| + | |
| − | \item[(h)]{$\displaystyle h_n=\sqrt{n^2+2n+3}-\sqrt{n^2+2n}$.}
| + | |
| − | \item[(i)]{$\displaystyle i_n=\frac{(2n+1)!n!}{(2n-1)!(n+1)!}$.}
| + | |
| − | \item[(j)]{$\displaystyle j_n=\frac{\sin n}{n}$.}
| + | |
| − | \item[(m)]{$\displaystyle m_n=\left( \frac{n+1}{n+4} \right)^n$.}
| + | |
| − | \end{description}
| + | |
| − | \textbf{Resolução:}
| + | |
| − | \begin{description}
| + | |
| − | \item[(a)]{ $\displaystyle \lim \frac{3n-5}{n+1}= \lim
| + | |
| − | \frac{n\left(3- \displaystyle \frac{5}{n}\right)}{n\left( 1+\displaystyle \frac{1}{n}\right)} =\lim \frac{3-\displaystyle \frac{5}{n}}{ 1+\displaystyle \frac{1}{n}}= \frac{3-0}{1+0} =3.$}
| + | |
| − | \item[(b)]{$\displaystyle \lim
| + | |
| − | \frac{4n^5+3n^2-n-5}{3n^2-2n+10} = \lim
| + | |
| − | \frac{n^2\left( 4n^3+3-\displaystyle \frac{1}{n}-\displaystyle \frac{5}{n^2} \right)}{n^2\left( 3-\displaystyle \frac{2}{n}+\displaystyle \frac{10}{n^2} \right)} = \lim
| + | |
| − | \frac{4n^3+3-\displaystyle \frac{1}{n}-\displaystyle \frac{5}{n^2}}{3-\displaystyle \frac{2}{n}+\displaystyle \frac{10}{n^2}}=+ \infty.$}
| + | |
| − | \item[(c)]{$\displaystyle \lim{(-n^2+n+7)}=\lim{n^2
| + | |
| − | \underbrace{\left( -1+\frac{1}{n}+\frac{7}{n^2}\right)}_{\begin{array}{c}\downarrow \\ {\tiny -1} \end{array}}} =- \infty.$}
| + | |
| − | \item[(d)]{$\displaystyle \lim
| + | |
| − | \frac{2^n-3^{n+2}}{2^{n-1}+3^{n+1}} = \lim
| + | |
| − | \displaystyle \frac{3^n\left(\left(\displaystyle\frac{2}{3}\right)^n-3^2\right)}{3^n\left(\left(\displaystyle \frac{2}{3}\right)^n \cdot 2^{-1}+3\right)}
| + | |
| − | = \lim \displaystyle \frac{\left(\displaystyle \frac{2}{3}\right)^n-3^2}{\left(\displaystyle \frac{2}{3}\right)^n \cdot 2^{-1}+3}
| + | |
| − | =\frac{0-9}{0+3}=-3.$}
| + | |
| − | \item[(e)]{Como $\sin (n \pi) =0$, para todo $n \in \mathbb{N}$,
| + | |
| − | então $\lim e_n=0$.}
| + | |
| − | \item[(f)]{Observe-se que:
| + | |
| − | \begin{itemize}
| + | |
| − | \item Se $n$ é da forma $1+4k$, vem, $\displaystyle f_{1+4k} = \sin{\frac{\pi}{2}}=1$
| + | |
| − | \item Se $n$ é da forma $2+4k$, vem, $\displaystyle f_{2+4k} = \sin{\pi}=0$
| + | |
| − | \item Se $n$ é da forma $3+4k$, vem, $\displaystyle f_{3+4k} = \sin{\frac{3\pi}{2}}=-1$
| + | |
| − | \item Se $n$ é da forma $4+4k$, vem, $\displaystyle f_{4+4k} = \sin{2\pi}=0$
| + | |
| − | \end{itemize} com $k=0,1,2, \ldots$.
| + | |
| − | | + | |
| − | Então $f_n$ toma somente os valores $1,0,-1$. Logo não existe limite da sucessão dada porque podemos escolher subsucessões de $(f_n)_n$ com limites distintos.}
| + | |
| − | \item[(g)]{Para $n$ par, $\displaystyle
| + | |
| − | g_n=\frac{-n+1}{n^3+1}$ e para $n$ ímpar, $\displaystyle
| + | |
| − | g_n=\frac{n+1}{n^3+1}$. Como $\displaystyle \lim \frac{-n+1}{n^3+1}
| + | |
| − | = \lim \frac{n+1}{n^3+1} =0$, resulta que $\lim g_n=0$.}
| + | |
| − | | + | |
| − | \vspace{2mm}
| + | |
| − | | + | |
| − | \item[(h)]{$\displaystyle \lim
| + | |
| − | (\sqrt{n^2+2n+3}-\sqrt{n^2+2n}) $
| + | |
| − | $\displaystyle =\lim
| + | |
| − | \frac{(\sqrt{n^2+2n+3}-\sqrt{n^2+2n})(\sqrt{n^2+2n+3}+\sqrt{n^2+2n})}{\sqrt{n^2+2n+3}+\sqrt{n^2+2n}}=$
| + | |
| − | $\displaystyle = \lim
| + | |
| − | \frac{(n^2+2n+3)-(n^2+2n)}{\sqrt{n^2+2n+3}+\sqrt{n^2+2n}}=$
| + | |
| − | $\displaystyle \lim \frac{3}{\sqrt{n^2+2n+3}+\sqrt{n^2+2n}}=0.$}
| + | |
| − | | + | |
| − | \vspace{2mm}
| + | |
| − | | + | |
| − | \item[(i)]{$\displaystyle \lim
| + | |
| − | \frac{(2n+1)!n!}{(2n-1)!(n+1)!} = \lim
| + | |
| − | \frac{(2n+1)(2n)(2n-1)!n!}{(2n-1)!(n+1)n!} = \lim
| + | |
| − | \frac{(2n+1)(2n)}{n+1}= + \infty$}
| + | |
| − | | + | |
| − | \vspace{2mm}
| + | |
| − | \item[(j)]{Como $-1 \leq \sin n \leq 1$, então
| + | |
| − | $\displaystyle \frac{-1}{n} \leq \frac{\sin n}{n} \leq \frac{1}{n}$.
| + | |
| − | Pelo teorema das sucessões enquadradas, como $\displaystyle \lim \frac{-1}{n}= \lim \frac{1}{n}=0$,
| + | |
| − | concluímos que
| + | |
| − | $\displaystyle \lim \frac{\sin n}{n}=0$.}
| + | |
| − | \vspace{2mm}
| + | |
| − | \item[(m)]{Procedendo à divisão de $n+1$ por
| + | |
| − | $n+4$, obtemos $\displaystyle \frac{n+1}{n+4}=1+\frac{-3}{n+4}$.
| + | |
| − | Logo $$\displaystyle \lim \left( \frac{n+1}{n+4} \right) ^n= \lim
| + | |
| − | \left[ \left( 1+\frac{-3}{n+4} \right)^{n+4} \cdot \left(
| + | |
| − | 1+\frac{-3}{n+4} \right)^{-4} \right]= e^{-3} \cdot
| + | |
| − | 1^{-4}=e^{-3}.$$}
| + | |
| − | \end{description}
| + | |
| − | | + | |
| − | | + | |
| − | \subsubsection*{Exercícios Resolvidos}
| + | |
| − | | + | |
| − | Seja $(a_n)_{n \in \mathbb{N}}$ a sucessão definida por
| + | |
| − | recorrência
| + | |
| − | $$\left\{ \begin{array}{ll}
| + | |
| − | a_1=3 & \\
| + | |
| − | \displaystyle a_{n+1}=\frac{1}{2}a_n+4, & \mbox{ para } n \geq 1\\
| + | |
| − | \end{array} \right.$$
| + | |
| − | Sabendo que a sucessão converge, determine o seu limite.
| + | |
| − | | + | |
| − | \textbf{Resolução:} Designemos por $L$ o valor do limite. Como a sucessão converge, $\lim a_n = \lim a_{n+1}$ e portanto $$\lim a_{n+1}= \lim
| + | |
| − | \left(\frac{1}{2}a_n+4\right) \Leftrightarrow L=\frac{1}{2}L+4 \Leftrightarrow L=8.$$ Logo a
| + | |
| − | sucessão converge para $8$.
| + | |
| − | | + | |
| − | \subsubsection*{Exercícios Resolvidos}
| + | |
| − | | + | |
| − | Sejam $a \in ]-1,1[$ e $b \in \mathbb{R}$. Considere a sucessão $(s_n)_{n \in \mathbb{N}}$ de termo geral
| + | |
| − | $$s_n=b(1+a+a^2+\ldots + a^{n-1}).$$ Mostre que $$\lim s_n=\frac{b}{1-a}.$$
| + | |
| − | | + | |
| − | \textbf{Resolução:} Se $a=0$, é óbvio.
| + | |
| − | | + | |
| − | Suponhamos agora que $a
| + | |
| − | \not=0$. Uma vez que $1+a+a^2+\ldots + a^{n-1}$ é a soma consecutiva
| + | |
| − | de termos de uma progressão geométrica de razão $a$, então
| + | |
| − | $$1+a+a^2+\ldots + a^{n-1}=\frac{1-a^n}{1-a}.$$ Como $|a|<1$, esta
| + | |
| − | sucessão converge para $\displaystyle \frac{1}{1-a}$. Logo $$\lim
| + | |
| − | s_n=\frac{b}{1-a}.$$
| + | |
| − | | + | |
| − | | + | |
| − | \subsubsection*{Exercícios Resolvidos}
| + | |
| − | | + | |
| − | Calcule o limite da sucessão cujos primeiros termos são
| + | |
| − | $$\sqrt{2}, \sqrt{2 \sqrt{2}}, \sqrt{2 \sqrt{2 \sqrt{2}}}, \ldots$$
| + | |
| − | | + | |
| − | \textbf{Resolução:} Designemos por $a_n$ o termo geral desta
| + | |
| − | sucessão. Então
| + | |
| − | $$\begin{array}{l}
| + | |
| − | a_1=2^{\frac{1}{2}}\\
| + | |
| − | a_2=\left(2\cdot 2^{\frac{1}{2}}\right)^{\frac{1}{2}}=2^{\frac{1}{2}+\frac{1}{4}}\\
| + | |
| − | a_3=\left(2 \cdot 2^{\frac{1}{2}+\frac{1}{4}}\right)^{\frac{1}{2}}=2^{\frac{1}{2}+\frac{1}{4}+\frac{1}{8}}\\
| + | |
| − | \vdots
| + | |
| − | \end{array}$$
| + | |
| − | De um modo geral
| + | |
| − | $$a_n=2^{\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+ \ldots
| + | |
| − | +\frac{1}{2^n}}.$$ Como $$\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+ \ldots
| + | |
| − | +\frac{1}{2^n}$$ é a soma consecutivas dos termos de uma progressão geométrica de razão $1/2$, temos que
| + | |
| − | $$\lim \left(
| + | |
| − | \frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+ \ldots
| + | |
| − | +\frac{1}{2^n}\right) = \lim \left( \frac{1}{2} \cdot
| + | |
| − | \frac{1-\left(\frac{1}{2}\right)^n}{1-\frac{1}{2}} \right) = 1,$$ então $\lim a_n=2^{\lim \left(
| + | |
| − | \frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+ \ldots
| + | |
| − | +\frac{1}{2^n}\right) }=2^1=2$.
| + | |
| − | | + | |
| − | | + | |
| − | \subsubsection*{Exercícios Propostos}
| + | |
| − | | + | |
| − | \begin{enumerate}
| + | |
| − | \item{Escreva os $5$ primeiros termos das seguintes sucessões:
| + | |
| − | \begin{enumerate}
| + | |
| − | \item{$\displaystyle a_n=\frac{3 \cdot (-1)^n}{n!}$;}
| + | |
| − | \item{$\displaystyle a_n=\cos \left( \frac{n \pi}{4} \right)$;}
| + | |
| − | \item{$\displaystyle a_1=4 \mbox{ e } a_{n+1}=\frac{1}{1+a_n}, n \in \mathbb{N}$;}
| + | |
| − | \item{$\displaystyle a_n=\sum_{i=1}^n(-1)^i$;}
| + | |
| − | \item{$\displaystyle a_n=\frac{1}{2}+ \left( \frac{1}{2} \right)^2+ \ldots + \left( \frac{1}{2} \right)^n$.}
| + | |
| − | \end{enumerate}
| + | |
| − | }
| + | |
| − | | + | |
| − | \item{Estude a monotonia de cada uma das seguintes sucessões e verifique se são limitadas:
| + | |
| − | \begin{enumerate}
| + | |
| − | \item{$\displaystyle a_n=\frac{1}{5^n}$;}
| + | |
| − | \item{$\displaystyle a_n=\frac{2n-3}{3n+4}$;}
| + | |
| − | \item{$\displaystyle a_n=\cos \left( \frac{n \pi}{2} \right)$;}
| + | |
| − | \item{$\displaystyle a_n=1- \left( \frac{3}{2} \right)^n$;}
| + | |
| − | \item{$\displaystyle a_n=3+ \frac{(-1)^n}{n}$;}
| + | |
| − | \item{$\displaystyle a_n=\frac{ \displaystyle \left(\frac{3}{2}\right)^n}{n!}$;}
| + | |
| − | \item{$\displaystyle a_n=\frac{n^2+1}{n}$.}
| + | |
| − | \end{enumerate}
| + | |
| − | }
| + | |
| − | | + | |
| − | | + | |
| − | \item{Averiguúe se cada uma das seguintes sucessões é convergente ou divergente, e no caso de convergência, indique
| + | |
| − | o respectivo limite.
| + | |
| − | \begin{enumerate}
| + | |
| − | \item{$\displaystyle a_n=n(n-1)$;}
| + | |
| − | \item{$\displaystyle a_n=\frac{3+5n^2}{n+n^2}$;}
| + | |
| − | \item{$\displaystyle a_n=\frac{\sqrt{n}}{n+1}$;}
| + | |
| − | \item{$\displaystyle a_n=\frac{2^n}{3^{n+1}}$;}
| + | |
| − | \item{$\displaystyle a_n=\frac{(-1)^n(n+2)}{n^3+4}$;}
| + | |
| − | \item{$\displaystyle a_n=\left(1+\frac{3}{n+2} \right)^{2n+1}$;}
| + | |
| − | | + | |
| − | \vspace{2mm}
| + | |
| − | \item{$\displaystyle a_n=\ln(n+1)- \ln (n)$;}
| + | |
| − | \item{$\displaystyle a_n=\frac{\cos ^2(n)}{2^n}$.}
| + | |
| − | \end{enumerate}
| + | |
Consideremos a sucessão real $\displaystyle a_n=1+\frac{1}{n}$. O seu gráfico é o seguinte:
O que se verifica é que, à medida que $n$ aumenta, o valor de $a_n$ aproxima-se de $1$. Escrevemos $\displaystyle \lim_{n
\to + \infty} a_n =1$ ou simplesmente $\displaystyle \lim a_n =1$.
Seja $(a_n)_{n \in \mathbb{N}}$ uma sucessão real. Dizemos que a sucessão é convergente se existe um número real $L$ tal que, à medida que $n$ cresce, os termos da sucessão aproximam-se de $L$. Escrevemos $\lim a_n =L$.
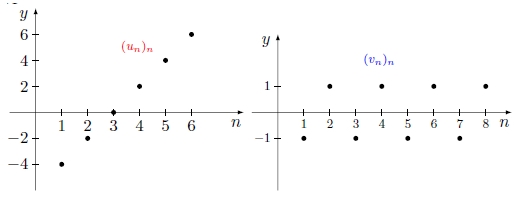
Os termos da sucessão $(u_n)_n$ aumentam indefinidamente; dizemos que $\displaystyle \lim u_n= +\infty$.
Os termos da sucessão $(v_n)_n$ vão oscilando entre $-1$ e $1$ consoante $n$ é ímpar ou par, respetivamente. Uma vez que o
limite de uma sucessão quando existe é único, concluímos que esta sucessão não tem limite.