Matemática Elementar
(→Conjuntos de números) |
|||
| Line 20: | Line 20: | ||
|||||| looong cell 8|| | |||||| looong cell 8|| | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
Revision as of 09:15, 2 October 2012
Contents |
Números e conjuntos
Conjuntos de números
Um conjunto é uma colecção de objectos, designados elementos, usualmente representado por uma letra maiúscula. Os conjuntos podem representar-se em extensão, $A=\{2, 4, 6, 8, 10\}$, ou em compreensão, $A=\{\mbox{números pares compreendidos entre 2 e 10} \}$. O uso de chavetas indica que se trata de um conjunto: $A$ é o conjunto dos números pares compreendidos entre 2 e 10. Quando queremos representar um conjunto com um número infinito de elementos usam-se $\ldots$. Por exemplo, $B=\{ \mbox{números ímpares}\}$ podemos representá-lo em extensão da seguinte forma $\{1,3,5,7,9, \ldots \}$.
Um conjunto sem elementos designa-se por conjunto vazio e representa-se por $\{ \}$ ou $\emptyset$.
Um conjunto $A$ diz-se que está contido num conjunto $B$ ou que é subconjunto de $B$ se cada elemento de $A$ é elemento de $B$. Por exemplo, se $A=\{\mbox{manga, ananás}\}$ e $B= \{\mbox{frutos tropicais}\}$, então $A$ é subconjunto de $B$ (ou $A$ está contido em $B$) e escreve-se $A\subseteq B$.
Os conjuntos numéricos mais utilizados estão descritos na tabela seguinte:
||Notação ||Definição ||Exemplos|| || cell 1 || cell 2 || cell 3 || |||| long cell 4 || cell 5 || ||cell 6 |||| long cell 7 || |||||| looong cell 8||
\begin{center} \begin{tabular}{|c|c|c|} \hline \textbf{Notação} & \textbf{Definição} & \textbf{Exemplos}\\ \hline UNIQ3f170e7411cb8644-MathJax-22-QINU & Números Naturais & UNIQ3f170e7411cb8644-MathJax-23-QINU \\ \hline UNIQ3f170e7411cb8644-MathJax-24-QINU & \centering Números Naturais e o Zero & UNIQ3f170e7411cb8644-MathJax-25-QINU \\ \hline UNIQ3f170e7411cb8644-MathJax-26-QINU & \centering Números Inteiros & UNIQ3f170e7411cb8644-MathJax-27-QINU \\ \hline UNIQ3f170e7411cb8644-MathJax-28-QINU & \centering Números Racionais & \begin{tabular}{|c|} dízimas finitas \\ UNIQ3f170e7411cb8644-MathJax-29-QINU \\ \hline dízimas infinitas periódicas: \\ UNIQ3f170e7411cb8644-MathJax-30-QINU \\ \end{tabular}\\ \hline UNIQ3f170e7411cb8644-MathJax-31-QINU & \centering Números Reais & UNIQ3f170e7411cb8644-MathJax-32-QINU; \\ (irracional ou dízima infinita não periódica) & & UNIQ3f170e7411cb8644-MathJax-33-QINU \\ \hline % UNIQ3f170e7411cb8644-MathJax-34-QINU & \centering Números Complexos\\ UNIQ3f170e7411cb8644-MathJax-35-QINU} & UNIQ3f170e7411cb8644-MathJax-36-QINU \\ \hline \end{tabular} \end{center}
Entre estes conjuntos verificam-se as seguintes inclusões: $$\mathbb{N} \subset \mathbb{N}_0 \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R}$$
Intervalos de números reais
Os intervalos de números reais são conjuntos muito importantes na matemática. O conjunto de números reais $x$ maiores do que $2$ e menores do que $5$, $2 < x < 5$ é o intervalo aberto $]2,5[=\{x \in \mathbb{R}: 2 < x < 5 \}$. Contudo, se considerarmos o conjunto dos números reais maiores ou iguais a 2 e menores do que 5 teremos $[2,5[=\{x \in \mathbb{R}: 2 \le x < 5 \}$; e se tomarmos o conjunto dos números reais maiores do que 2 e menores ou iguais a 5 teremos o intervalo $]2,5]=\{x \in \mathbb{R}: 2 < x \le 5 \}$. O intervalo fechado $[2,5]=\{x \in \mathbb{R}: 2 \le x \le 5 \}$ corresponde ao conjunto dos números reais maiores ou iguais a 2 e menores ou iguais a 5.
O subconjunto dos números reais que consiste em todos os números reais $x$ que estão entre $a$ e $b$ pode ser representado pela dupla desigualdade $a < x < b$ e, em termos de conjunto, pelo intervalo $]a,b[ = \{ x \in \mathbb{R} : a < x < b \}$ , designado por intervalo aberto.
Caso as extremidades $a$ e $b$ estejam incluídas representa-se o intervalo por $[a,b]= \{ x \in \mathbb{R} : a \le x \le b \}$ e designa-se por intervalo fechado.
Os intervalos contendo apenas uma das extremidades, $]a,b]$ ou $[a,b[$ designam-se por intervalos semi-abertos:
$]a,b]= \{ x \in \mathbb{R} : a < x \le b \} \qquad [a,b[ = \{ x \in \mathbb{R} : a \le x < b \}$
Podemos ainda usar os intervalos $[a,+ \infty [$ e $]-\infty, b]$ para representar em termos de conjuntos as desigualdades
$[a,+ \infty [=\{ x \in \mathbb{R}: x \ge a \} \qquad ]-\infty, b]=\{ x \in \mathbb{R}: x \le b \}$
Os intervalos de números reais podem ser usados para representar os números negativos ou os números positivos
$\mathbb{R}^+=\{x\in\mathbb{R}:x>0\}=]0,+\infty[ \qquad \mathbb{R}_0^+=\mathbb{R}^+\cup\{0\}=[0,+\infty[ \qquad \mathbb{R}^-=\{x\in\mathbb{R}:x<0\}=]-\infty,0[ \qquad\mathbb{R}_0^-=\mathbb{R}^-\cup\{0\}=]-\infty,0]$
Operações com conjuntos
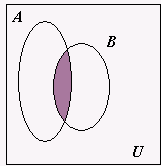
No que se segue apresentam-se algumas operações entre conjuntos. Assim, sejam $A$ e $B$ dois conjuntos do universo $U$. O conjunto que contém os elementos comuns aos dois conjuntos $A$ e $B$ é conhecido como intersecção dos dois conjuntos, $A \cap B = \{x \in U : x \in A \mbox{ e } x \in B \}$:
Se a intersecção de dois conjuntos é o vazio, significa que os conjuntos não possuem elementos em comum e, neste caso os conjuntos dizem-se \textbf{disjuntos}.
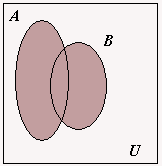
A reunião (ou união) de dois conjuntos $A$ e $B$ é o conjunto que contém todos os elementos dos dois conjuntos, $A \cup B = \{x \in U : x \in A \mbox{ ou } x \in B \}$ .
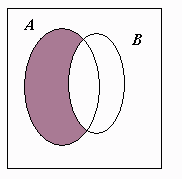
Designa-se por $A-B$ ou $A \backslash B$ o conjunto que contém todos os elementos de $A$, excepto os que pertencem a $B$, $A \backslash B = \{ x \in U : x \in A \mbox{ e } x \notin B \}$.
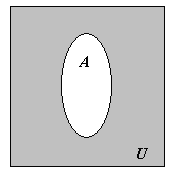
Todos os elementos do conjunto universo que não pertencem ao conjunto $A$ formam um conjunto chamado complementar de $A$, o qual se representa por $A^{\emph{C}}$ ou $\overline{A}$, $\overline{A} = \{ x \in U : x \notin A \}$.
Insert non-formatted text here
MediaWiki has been successfully installed.
Consult the User's Guide for information on using the wiki software.