Função módulo
(→A função módulo) |
(→A função módulo) |
||
| Line 12: | Line 12: | ||
[[Exemplo 18|Exemplo]] | [[Exemplo 18|Exemplo]] | ||
| − | |||
| − | |||
| − | + | [[Outros exemplos]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
Revision as of 15:45, 6 November 2012
A função módulo
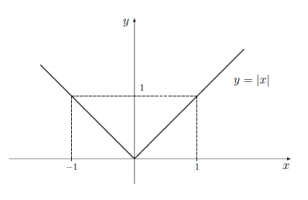
A função módulo pode ser encarada como uma função definida por ramos:
Esta função é contínua (o gráfico não tem "saltos"), tem um zero em $x=0$, é decrescente em $]-\infty,0[$ e crescente em $]0,+\infty[$. $(0,f(0))=(0,0)$ é um mínimo local e global da função.
A representação gráfica da função módulo pode ajudar na resolução de problemas algébricos, como o exemplo seguinte ilustra.
\subsubsection*{Exercícios Resolvidos}
Seja $f$ a função definida por $f(x)=|x^2-3x+2|$.
\begin{description}
\item[(a)] Reescreva a expressão analítica de UNIQ2b01ed2561a31aa7-MathJax-14-QINU sem usar o símbolo UNIQ2b01ed2561a31aa7-MathJax-15-QINU.
\item[(b)]Determine o conjunto UNIQ2b01ed2561a31aa7-MathJax-16-QINU por forma a que a proposição ``UNIQ2b01ed2561a31aa7-MathJax-17-QINU" \ seja verdadeira.
\end{description}
\textbf{Resolução:} \begin{description} \item[(a)] Comecemos por analisar o sinal de UNIQ2b01ed2561a31aa7-MathJax-18-QINU. UNIQ2b01ed2561a31aa7-MathJax-1-QINU O produto será positivo se os dois factores tiverem o mesmo sinal e negativo se os factores tiverem sinais contrários. Então: UNIQ2b01ed2561a31aa7-MathJax-2-QINU UNIQ2b01ed2561a31aa7-MathJax-3-QINU Podemos agora definir a função UNIQ2b01ed2561a31aa7-MathJax-19-QINU por ramos da seguinte forma: UNIQ2b01ed2561a31aa7-MathJax-4-QINU Repare que UNIQ2b01ed2561a31aa7-MathJax-20-QINU sendo portanto indiferente calcular o valor da função nestes pontos num ou noutro ramo. \item[(b)] Pretende-se determinar o conjunto UNIQ2b01ed2561a31aa7-MathJax-5-QINU Resolvendo as duas inequações temos: {\small UNIQ2b01ed2561a31aa7-MathJax-6-QINU } O conjunto UNIQ2b01ed2561a31aa7-MathJax-21-QINU é a intersecção dos conjuntos solução das duas inequações, UNIQ2b01ed2561a31aa7-MathJax-7-QINU \end{description}
\subsubsection*{Exercícios Propostos}
\begin{enumerate}
\item Reescreva a expressão analítica das seguintes funções, sem usar o símbolo módulo:
\begin{description}
\item[(a)] UNIQ2b01ed2561a31aa7-MathJax-22-QINU;
\item[(b)] UNIQ2b01ed2561a31aa7-MathJax-23-QINU
\end{description}
\item
Utilize o processo gráfico para resolver as inequações:
\begin{description}
\item[(a)] UNIQ2b01ed2561a31aa7-MathJax-24-QINU;
\item[(b)] UNIQ2b01ed2561a31aa7-MathJax-25-QINU.
\end{description}
\end{enumerate}