Operações com conjuntos
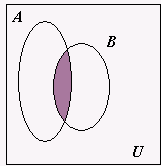
No que se segue apresentam-se algumas operações entre conjuntos. Assim, sejam $A$ e $B$ dois conjuntos do universo $U$. O conjunto que contém os elementos comuns aos dois conjuntos $A$ e $B$ é conhecido como interseção dos dois conjuntos, $A \cap B = \{x \in U : x \in A \mbox{ e } x \in B \}$:
Se a interseção de dois conjuntos é o vazio, significa que os conjuntos não possuem elementos em comum e, neste caso os conjuntos dizem-se disjuntos.
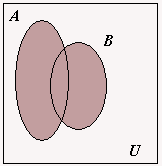
A reunião (ou união) de dois conjuntos $A$ e $B$ é o conjunto que contém todos os elementos dos dois conjuntos, $A \cup B = \{x \in U : x \in A \mbox{ ou } x \in B \}$ .
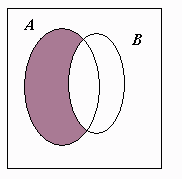
Designa-se por $A-B$ ou $A \backslash B$ o conjunto que contém todos os elementos de $A$, excepto os que pertencem a $B$, $A \backslash B = \{ x \in U : x \in A \mbox{ e } x \notin B \}$.
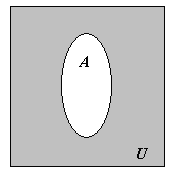
Todos os elementos do conjunto universo que não pertencem ao conjunto $A$ formam um conjunto chamado complementar de $A$, o qual se representa por $A^{C}$ ou $\overline{A}$, $\overline{A} = \{ x \in U : x \notin A \}$.
Exemplo: Se considerar $A=[-1,3[$ e $B=]0, + \infty [$, tem-se:
$\begin{array}{ccc} & & \\ A \cap B = ]0,3[ & A \cup B = [-1, + \infty [ & A^{\cal{C}} = \overline{A} = ]- \infty, -1[ \cup [3, + \infty [ \\ & & \\ B^{\cal{C}} = \overline{B} = ]- \infty , 0] & A-B = A \backslash B = [-1,0] & B-A = B \backslash A = [3, + \infty [ \\ \end{array}$
Condições
Uma condição (numérica) é uma expressão que contém variáveis e que, para toda a concretização (substituição das variáveis por números), só admite um valor lógico, verdadeiro (V) ou falso (F).
Chama-se 'condição universal (CU) a uma condição que é verdadeira para toda a concretização (p.e., $x^2+1>0$); chama-se condição impossível (CI) a uma condição que é falsa para toda a concretização (p.e., $x^2+1 \le 0$).
A partir de condições elementares (por exemplo, relações de igualdade, $=$, ou de ordem, $<$), constroem-se condições mais complicadas por conjunção (com o operador $\land$, "e") ou disjunção (com o operador $\lor$, "ou").
- À conjunção de condições ($\land$) corresponde a interseção de conjuntos solução ($\cap$).
- À disjunção de condições ($\lor$) corresponde a reunião de conjuntos solução ($\cup$).
Exemplos
- $x > 0 $ e $x \le 1$, é equivalente à condição $0<x \le 1$;
- $x +1=5 $ ou $x-2 <0$, é equivalente à condição $x \in ]-\infty , 2[ \cup \{4\}$;
- $x+2<0$ e $x+2 \ge 0$ é uma condição impossível. O seu conjunto solução é o conjunto vazio, $\emptyset $;
- $x+2<0$ ou $x+2 \ge 0$ é uma condição universal. O seu conjunto solução é o conjunto $\mathbb{R} $.
Podem formular-se as seguintes leis:
Seja $C$ uma condição qualquer, $CI$ uma condição impossível, $CU$ uma condição universal. Então,
- $C\land CI$ é $CI$: a conjunção de uma condição qualquer com uma condição impossível é uma condição impossível.
- $\underbrace{x+1=0}_{C}\land \underbrace{x^2+1=0}_{CI}$
- $\underbrace{x+1=0}_{C}\land \underbrace{1=0}_{F}$
são Condições Impossíveis.
- $C\lor CU$ é CU: A disjunção de uma condição qualquer com uma condição universal é uma condição universal.
- $\underbrace{x+1=0}_{ C}\lor \underbrace{x^2+1>0}_{CU}$ e
- $\underbrace{x+1=0}_{ C}\lor \underbrace{1>0}_V$
são Condições Universais.
- $ C\lor CI$ e $ C\land CU$ são equivalentes a $C$, porque os conjuntos solução coincidem com o conjunto solução de $C$.