Convergência de uma sucessão
Convergência de uma sucessão
Consideremos a sucessão real $\displaystyle a_n=1+\frac{1}{n}$. O seu gráfico é o seguinte:
O que se verifica é que, à medida que $n$ aumenta, o valor de $a_n$ aproxima-se de $1$. Escrevemos $\displaystyle \lim_{n \to + \infty} a_n =1$ ou simplesmente $\displaystyle \lim a_n =1$.
Seja $(a_n)_{n \in \mathbb{N}}$ uma sucessão real. Dizemos que a sucessão é convergente se existe um número real $L$ tal que, à medida que $n$ cresce, os termos da sucessão aproximam-se de $L$. Escrevemos $\lim a_n =L$.
Formalmente, dizemos que a sucessão converge para $L$ se
$$\forall \epsilon >0, \hspace{.2cm }\exists N \in \mathbb{N} \hspace{.2cm}:
\hspace{.2cm} n \geq N \to |a_n-L|< \epsilon$$
Se tal real $L$ não existe, dizemos que a sucessão é divergente.
O limite de uma sucessão, se existir, é único.
Por exemplo, tomemos as duas seguintes sucessões:
$$u_n=2n-6 \hspace{1cm} \mbox{e} \hspace{1cm} v_n=(-1)^n. $$
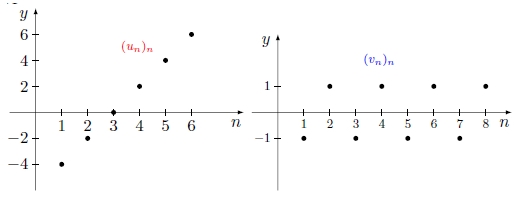
Os gráficos das duas sucessões são, respetivamente
Os termos da sucessão $(u_n)_n$ aumentam indefinidamente; dizemos que $\displaystyle \lim u_n= +\infty$.
Os termos da sucessão $(v_n)_n$ vão oscilando entre $-1$ e $1$ consoante $n$ é ímpar ou par, respetivamente. Uma vez que o limite de uma sucessão quando existe é único, concluímos que esta sucessão não tem limite.
Ambas as sucessões são divergentes.
Se $\lim a_n=+ \infty$ dizemos que a sucessão $(a_n)_n$ é um infinitamente grande positivo. Formalmente dizemos, $$\lim a_n=+ \infty \Leftrightarrow \forall M \in \mathbb{R}, \hspace{.2cm} \exists N \in \mathbb{N} \hspace{.2cm}: \hspace{.2cm} n \geq N \to a_n>M;$$ Se $\lim a_n=- \infty$ a sucessão diz-se um infinitamente grande negativo. Formalmente temos: $$\lim a_n=- \infty \Leftrightarrow\forall M \in \mathbb{R}, \hspace{.2cm} \exists N \in \mathbb{N} \hspace{.2cm}: \hspace{.2cm} n \geq N \to a_n<M;$$ Se $\lim a_n=0$ a sucessão é um infinitésimo. Formalmente, $$\lim a_n=0 \Leftrightarrow \forall \epsilon >0, \hspace{.2cm} \exists N \in \mathbb{N} \hspace{.2cm}: \hspace{.2cm} n \geq N \to |a_n|< \epsilon.$$