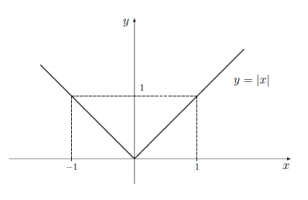
Função módulo
A função módulo
A função módulo pode ser encarada como uma função definida por ramos:
Esta função é contínua (o gráfico não tem "saltos"), tem um zero em $x=0$, é decrescente em $]-\infty,0[$ e crescente em $]0,+\infty[$. $(0,f(0))=(0,0)$ é um mínimo local e global da função.
A representação gráfica da função módulo pode ajudar na resolução de problemas algébricos, como o exemplo seguinte ilustra.
\subsubsection*{Exercícios Propostos} \begin{enumerate} \item Reescreva a expressão analítica das seguintes funções, sem usar o símbolo módulo: \begin{description} \item[(a)] UNIQ29230be46dcef817-MathJax-5-QINU; \item[(b)] UNIQ29230be46dcef817-MathJax-6-QINU \end{description} \item Utilize o processo gráfico para resolver as inequações: \begin{description} \item[(a)] UNIQ29230be46dcef817-MathJax-7-QINU; \item[(b)] UNIQ29230be46dcef817-MathJax-8-QINU. \end{description} \end{enumerate}