Máximos e mínimos
| Line 24: | Line 24: | ||
[[Exemplo 13|Exemplo]] | [[Exemplo 13|Exemplo]] | ||
| − | + | [[Matemática Elementar#Funções reais de variável real|Voltar]] [[Funções limitadas|Seguinte]] | |
| − | [[Matemática Elementar#Funções reais de variável real|Voltar]] | + | |
Revision as of 09:15, 19 November 2012
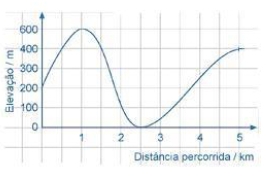
Consideremos agora o seguinte gráfico, que descreve um passeio do Filipe. No gráfico representa-se a variação da elevação do terreno, relativamente ao nível médio das águas do mar, com a distância percorrida pelo Filipe:
Observe-se que a curva representa uma função, porque a cada objeto corresponde uma só imagem. Quando o Flipe iniciou o passeio estava a uma altitude de 200m. Começou a subir até atingir um máximo de 600m, ao fim de 1km de percurso. Depois iniciou uma descida de 1.5km, até chegar a uma altitude mínima de 0m (nível médio das águas do mar). Iniciou de novo uma subida até atingir um novo máximo de 400m.
Se analisarmos este passeio do Filipe à luz das funções podemos afirmar que a função cresce até atingir um máximo de 600m ao fim de 1km percorrido. Depois decresce até atingir um mínimo de 0m, ao fim de 2.5km e começa de novo a crescer até atingir os 600m ao fim de 5km, quando termina o passeio. Os pontos onde a função passa de crescente a decrescente são máximos e passa de decrescente a crescente num ponto de mínimo.
Quando numa função acontecem situações como as descritas, ou seja, pontos que marcam a alteração de monotonia, dizemos que esses pontos são extremos locais da função. Assim para $x = a$ uma função $f$ tem:
- um máximo local quando em $a$ a função passa de crescente a decrescente;
- um mínimo local, quando em $a$ a função passa de decrescente a crescente.
Por outro lado, se para todo o $x$ pertencente ao domínio de $f$:
- existir $a \in D_f$ tal que $f(x) \ge f(a)$, dizemos que em $x=a$ a função tem um mínimo absoluto;
- existir $b$ no domínio de $f$ tal que $f(x) \le f(b)$, dizemos que em $x=b$ a função tem um máximo absoluto.
Os valores do domínio a que correspondem máximos da função chamam-se maximizantes ($b$ é um maximizante) e aos valores a que correspondem mínimos chamam-se minimizantes ($a$ é um minimizante).
Mais à frente daremos resultados que nos permitem determinar máximos e mínimos locais de uma função sem recorrer ao seu gráfico, bem como os intervalos de monotonia, isto é, indicar os intervalos onde a função é crescente e os intervalos onde a função é decrescente.