Círculo trigonométrico
Círculo trigonométrico
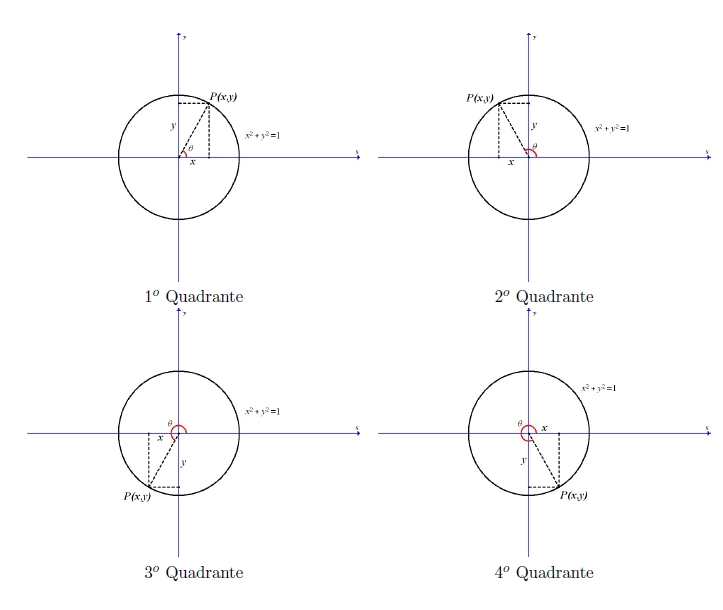
As funções trigonométricas representam fenómenos cíclicos devido à sua periodicidade. Para fazer o seu estudo vamos recorrer ao chamado círculo trigonométrico, um círculo de raio 1, onde são considerados os ângulos e podem ser representadas as respetivas razões trigonométricas.
Considerem-se dois eixos ortogonais $Ox$ e $Oy$. Relativamente a este sistema de eixos coordenados, os ângulos orientados têm uma posição em que o vértice está na origem das coordenadas e o lado origem coincide com o semi-eixo positivo $Ox$. Nestas condições, diz-se que o ângulo é do $1^o$, $2^o$, $3^o$ ou $4^o$ quadrante conforme o lado extremidade se situe num daqueles quadrantes, respetivamente.
Para definirmos as funções trigonométricas, como funções reais de variável real, os ângulos $\theta$ devem estar expressos em radianos e não em graus.
Como o perímetro de um círculo de raio $r$ é $2\pi r$, se $r=1$, o perímetro é $2 \pi$, correspondendo assim $2 \pi$ a $360^o$. A partir daqui podemos exprimir qualquer ângulo em radianos usando uma regra de 3 simples.
$\theta$ (Graus) $0^o$ $30^o$ $45^o$ $60^o$ $90^o$ $180^o$ $270^o$ $360^o$ $\theta$ (Radianos) $0$ $\displaystyle \frac{\pi}{6}$ $\displaystyle \frac{\pi}{4}$ $\displaystyle \frac{\pi}{3}$ $\displaystyle \frac{\pi}{2}$ $\pi$ $\displaystyle \frac{3\pi}{2}$ $2 \pi$
Assim, os ângulos do $1^o$ quadrante têm amplitudes $\displaystyle 0 \le \theta \le \frac{\pi}{2}$, os do $2^o$ quadrante entre $\displaystyle \frac{\pi}{2} \le \theta \le \pi $, os do $3^o$ quadrante, $\displaystyle \pi \le \theta \le \frac{3\pi}{2}$ e os do $4^o$ quadrante, $\displaystyle \frac{3\pi}{2} \le \theta \le 2\pi$.