 |
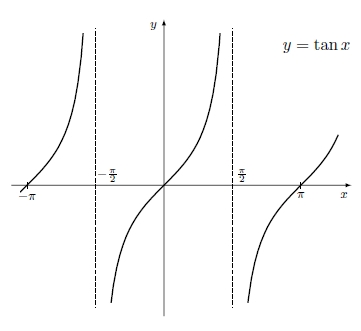
- Domínio: $\left\{x \in \mathbb{R}: x \neq \frac{\pi}{2}+k\pi, k \in \mathbb{Z}\right\}$
- Contradomínio: $\mathbb{R}$
- $\tan{(-x)}=-\tan x , \forall x \in \mathbb{R}$ (a função é ímpar)
- A função é periódica de período $ \pi$: $\tan{(x+k\pi)}=\tan{x}, \forall k \in \mathbb{Z}$
- Zeros: $\tan{x}=0 \Leftrightarrow x = k\pi, k \in \mathbb{Z}$
- A função tangente não tem máximo nem mínimo
- A função tem como assímptotas verticais as rectas $\displaystyle x=\frac{\pi}{2}+k\pi, \mbox{ com }k \in \mathbb{Z}$
|